
Rotating Shafts - Torque - Torsional moments acting on rotating shafts.Modulus of Rigidity - Shear Modulus (Modulus of Rigidity) is the elasticity coefficient for shearing or torsion force.Mild Steel - Round Bar - Weight of round bars.mass of object, it's shape and relative point of rotation - the Radius of Gyration. Mass Moment of Inertia - The Mass Moment of Inertia vs.Improvised Torque Wrench - Improvise a torque wrench with a luggage scale.Statics - Loads - forces and torque, beams and columns.Mechanics - Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.Minimum diameter of the shaft can be calculated with eq. Re-arranged and with values - the torque can be calculated The connection between power and torque can be expressed The maximum allowable shear stress - τ max - in the shaft is 100 MPa. The motor and the shaft rotates with 2000 rpm. = 1.4 o Example - Required Shaft Diameter to Transmit PowerĪ 15 kW electric motor shall be used to transmit power through a connected solid shaft. The shaft is made in steel with modulus of rigidity 79 GPa (79 10 9 Pa). = 1.2 o Example - Shear Stress and Angular Deflection in a Hollow CylinderĪ moment of 1000 Nm is acting on a hollow cylinder shaft with outer diameter 50 mm (0.05 m), inner diameter 30 mm (0.03 m) and length 1 m. The angular deflection of the shaft can be calculated as Maximum shear stress can be calculated as (π / 16) τ max ((2 R) 4 - (2 r) 4) / (2 R)Įxample - Shear Stress and Angular Deflection in a Solid CylinderĪ moment of 1000 Nm is acting on a solid cylinder shaft with diameter 50 mm (0.05 m) and length 1 m. Α degrees ≈ 584 L T / (G (D 4- d 4) (6b) Torsion Resisting Moments from Shafts of Various Cross Sections The angle in degrees can be achieved by multiplying the angle θ in radians with 180 / π. The angular deflection of a torsion hollow shaft can be expressed as The angular deflection of a torsion solid shaft can be expressed as G = Shear Modulus of Rigidity - or Modulus of Rigidity (Pa, psf)

The angular deflection of a torsion shaft can be expressed as Polar Moment of Inertia of a circular hollow shaft can be expressed asĭ = shaft inside diameter (m, ft) Diameter of a Solid Shaftĭiameter of a solid shaft can calculated by the formulaĭ = 1.72 ( T max / τ max ) 1/3 (4) Torsional Deflection of Shaft Polar Moment of Inertia of a circular solid shaft can be expressed as T max = (π / 16) τ max (D 4 - d 4) / D (2c) Circular Shaft and Polar Moment of Inertia Τ max = maximum shear stress (Pa, lb f/ft 2)Ĭombining (2) and (3b) for a hollow shaft T max = maximum twisting torque (Nm, lb f ft) Maximum moment in a circular shaft can be expressed as:

" Area Moment of Inertia" - a property of shape that is used to predict deflection, bending and stress in beamsĬircular Shaft and Maximum Moment or Torque." Polar Moment of Inertia" - a measure of a beam's ability to resist torsion - which is required to calculate the twist of a beam subjected to torque.
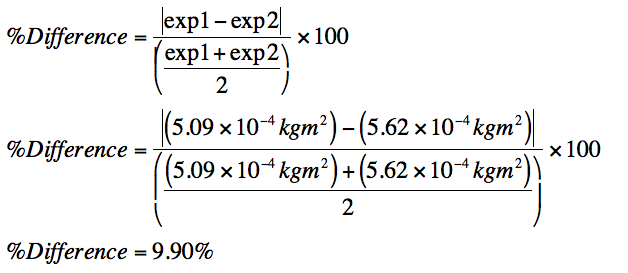
" Polar Moment of Inertia of an Area" is also called " Polar Moment of Inertia", " Second Moment of Area", " Area Moment of Inertia", " Polar Moment of Area" or " Second Area Moment". It is analogous to the " Area Moment of Inertia" - which characterizes a beam's ability to resist bending - required to predict deflection and stress in a beam. The " Polar Moment of Inertia" is defined with respect to an axis perpendicular to the area considered.


 0 kommentar(er)
0 kommentar(er)
